Exploring repunit digit sum fractions

In which I go down a rabbit hole of integer sequences when trying to understand a pattern in fractions of repeated digits and their digit sums.

The tweets

Note: this post was written when I was still using Twitter, I have since moved on to mastodon.

This tweet appeared in my Twitter feed:

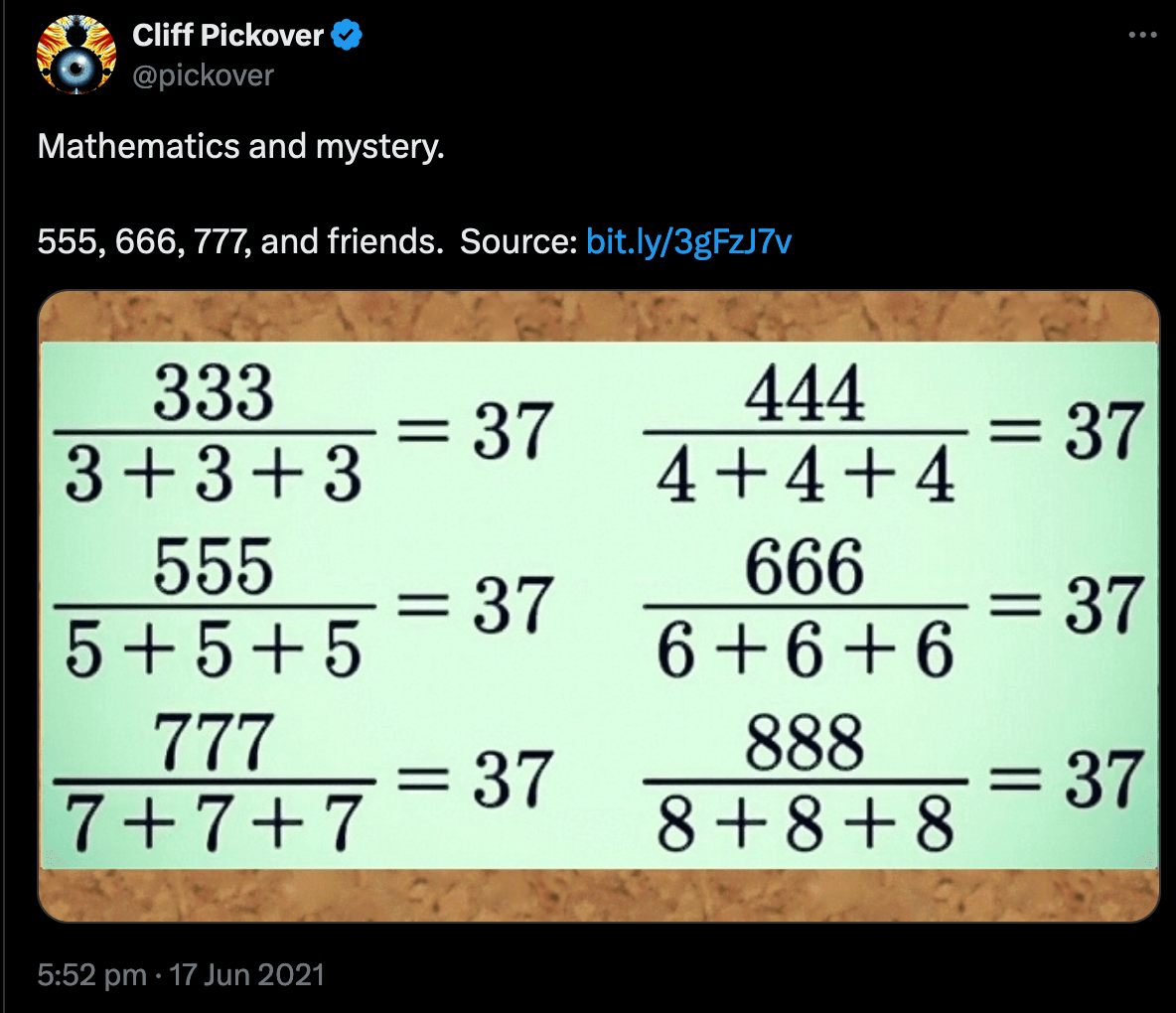
These are the fraction of a repdigit and the sum of its digits. My first thought was that I could write all these like this: \[ \frac{N}{N}\frac{111}{1+1+1}=37\,\quad\text{where } 0 \lt N \lt 10\,. \] Hence, these fractions are all repunits. A new question comes to mind: for which numbers of repeated digits n is the fraction an integer?

This handy formula from the Online Encylopedia of Integer Sequences (OEIS) A002275 generates repunits: \[ R_n=\frac{10^n - 1}{9}\,. \] As the sum in the denominator is just the number of digits, the fraction $Q$ then is \[ Q_n=\frac{R_n}{n} = \frac{10^n - 1}{9n}\,. \]

I made a python script to see when the result is an integer:

[(n, (10**n - 1)//9/n) for n in range(1, 10)]

which gives integer fractions for \(Q=1\) for \(n=1\), \(Q=37\) for \(n=3\), and \(Q=12345679\) for \(n=9\).

[(1, 1.0),
 (2, 5.5),
 (3, 37.0),
 (4, 277.75),
 (5, 2222.2),
 (6, 18518.5),
 (7, 158730.14285714287),
 (8, 1388888.875),
 (9, 12345679.0)]

I replied to the post with the case for \(n=9\), which led to this response:

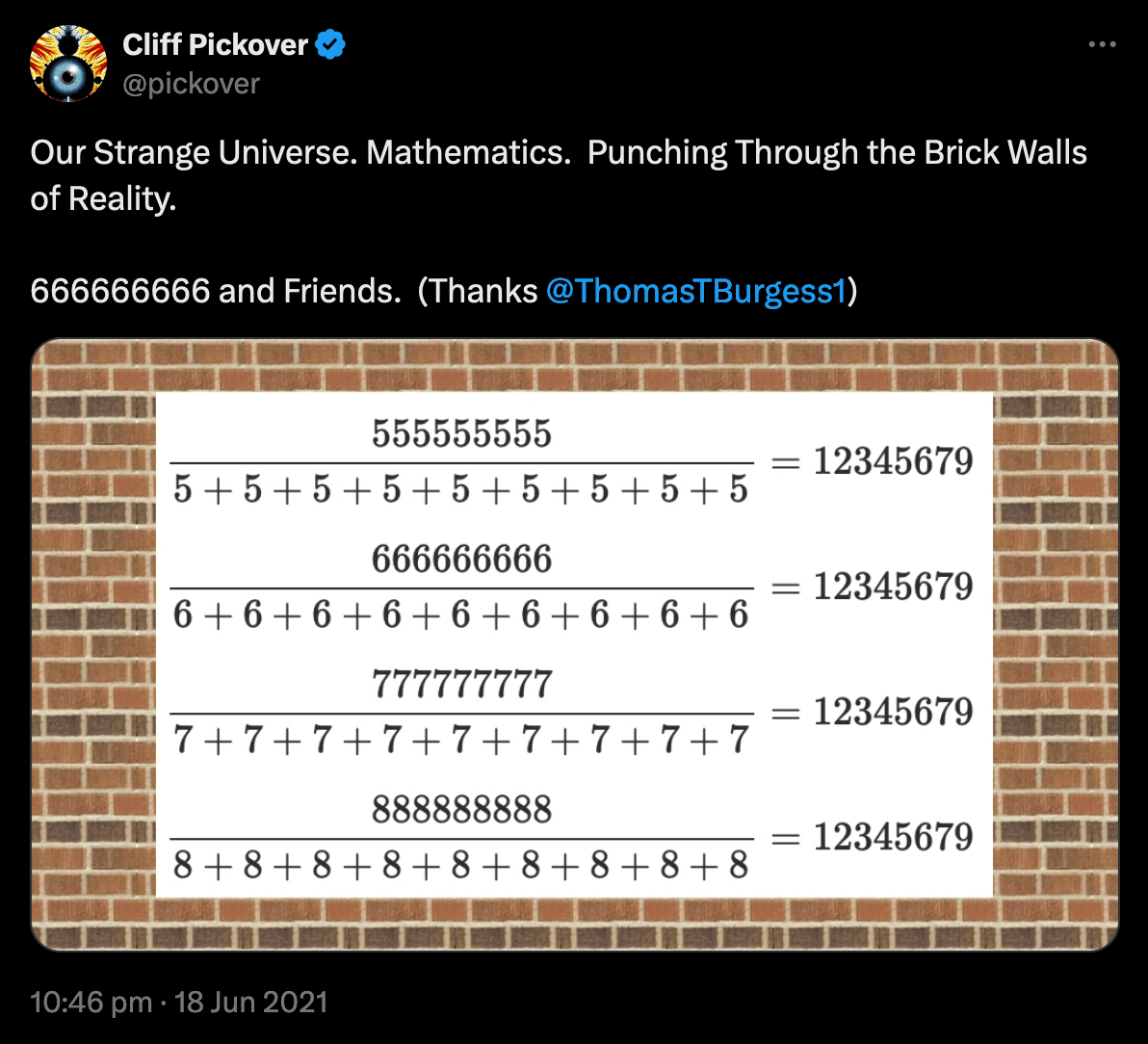
On a tangent, a typo in my first reply pointed out by @mikekohnstamm added the “missing” \(8\) to \(Q=12345679\). Furthermore, @Kapil_kant pointed out that the \(8\) is there if the fraction is: \[ \frac{1111111101}{1+1+1+1+1+1+1+1+0+1}=123456789\,. \] I’ll save investigating that for another time.

Going deeper

A better way to search for exact integer fractions is to check when the modulus is 0 and only print those cases using integer division. This is done in the following python snippets:

print("Q", [(10**n-1)//(9*n) for n in range(1, 200) if not (10**n-1)//9 % n])
print("denominators", [n for n in range(1, 20000) if not (10**n-1)//9 % n])

This gives the solution sequence \(Q=1, 37, 12345679, 4115226337448559670781893,\ldots\) with denominators \(1, 3, 9, 27, 81, 111, 243, ...\). Evidently \(Q(n)\) grows very fast with \(111\) terms already at \(n=6\).

  Q: [1, 37, 12345679, 4115226337448559670781893, 
    1371742112482853223593964334705075445816186556927297668038408779149519890260631, 
    10010010010010010010010010010010010010010010010010010010010010010010010010010010...
    01001001001001001001001001001]
  denominators [1, 3, 9, 27, 81, 111, 243, 333, 729, 999, 2187, 2997, 4107, 6561, 
    8991, 12321, 13203, 19683]

Several series repunit-related sequences mention these numbers: A190301, A215258, A215258. I couldn’t find this sequence in the OEIS, so I registered and made it my first submission.

Update 2021-08-02: it is now sequence A215258 - Ratios R(k)/k for which R(k) / k is an integer, where R(k) = A002275(k) is a repunit.

The sequence of denominators 1, 3, 9, 27, 81, …, suggests the conjecture: \(Q\) is integer when \(n\) is of the form \(n=3^n\). One OEIS editor proved this elegantly for me: \(R_{3n} / R_n = 10^{2n} + 10^n + 1\), which is divisible by 3. Therefore, \(R_{3^m}\) is divisible by \(3^m\) by induction on \(m\). However, there are additional solutions: 111, 333, 999, …. There is no known general rule for the denominator. The full sequence of denominators is A014950 in OEIS. Using this with the OEIS sequence for \(R_n\) (A002275), all the integer fractions are: \[ Q(n) = \frac{A002275(A014950(n))}{A014950(n)}\,. \]

My favourite integer fraction so far is: \[ Q(6)=\frac{R_{111}}{111} = \ldots \] \[ \tiny \frac{11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111}{111} = \ldots \] \[ \tiny 1001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001001 \]

Takeaway

Twitter (in 2021), if done right, can be a source of inspiration and knowledge. Also, recreational maths is fun.

Header image: repunit digit sum ratio remix of Ganymede from Juno.