Polygon vertices | Thomas T Burgess's Blog

Introduction

There are only 21 ways to place regular polygons in gapless tilings. The point where the polygons meet is called a vertex. Vertices are named by the polygons meeting there. For instance, the vertex where four squares meet is 4.4.4.4. In this post, I will make code to find and draw all possible vertices.

Regular polygons

A regular polygon has \(n\) sides. The interior angle \(\alpha\) between two adjacent sides is \begin{equation} \alpha=\frac{n-2}{2n}. \end{equation} The turning angle \(\beta=1/n\) of a polygon is the angle to the centre between two adjacent points. For simplicity, I write angles as fractions of a complete turn. Multiply by \(2\pi\) or \(360^\circ\) to get radians or degrees.

The pointiest polygon is the regular triangle with \(\alpha=1/6\). When increasing \(n\), \(\alpha\) increases towards \(1/2\).

Searching for vertices

For a tiling to be gapless, the sum of interior angles \(\alpha\) at a vertex must be 1. Thus, the complete set of vertices can be found by finding all sets \(v_i\) so that: \begin{equation} \sum_{n_j\in v_i} \frac{n_j-2}{2n_j} = 1\,. \end{equation}

Before searching, it helps to have ranges on the possible number of polygons \(m\) and sides \(n\) in \(v_i\). The count \(m\) must be larger than 2, as no two regular polygons can add up to 1. Furthermore, the highest \(m\) is six as 3.3.3.3.3.3 as \(\sum_{n \in 3.3.3.3.3.3} \alpha=6\cdot1/6=1\). For \(m=6\) this is the only possible vertex.

For \(m=3\), the two shape combination leaving the smallest angle \(\alpha\lt1/2\) is 3 and 7, as that 3 and 6 leaves exactly \(\alpha=1/2\), which can’t be a polygon. The remaining angle then is

\begin{equation} \alpha=1-\left(\alpha_3+\alpha_2\right)= 1-\left(\frac{3-2}{2\cdot3}+ \frac{7-2}{2\cdot7}\right)= \frac{10}{21}\,, \end{equation} and with \((n-2)/(2n)=10/21\) we get \(n=42\). Similarly for \(m=4\), 3.3.4 leaves \(\alpha\le1-(2/6+2/8)=5/12\), corresponding to \(n=12\). Finally for \(m=5\), 3.3.3.3 leaves \(\alpha\le1-(4/6)=1/3\), corresponding to \(n_5=6\).

In summary:

\[ m:3 \quad 3\le n\le 42
\] \[ m:4 \quad 3\le n\le 12
\] \[ m:5 \quad 3\le n\le 6
\] \[ m:6 \quad n=3 \]

All possible vertices are found by searching for combinations of \(m\) elements with \(n\) inside the constrained range. Note that this brute force approach will trivial clones of vertices in the form of rotations and mirror images. Moreover, there are some cases of different vertices with the same polygon content. Thus, I first generate (sorted) combinations with replacements of polygons for each \(m\). If a set sums to 1, I yield permutations not already stored as a mirror or rotation.

Python search implementation

For the search I only rely on python 3.8+ and its built in libraries. You don’t need to read the code unless you’re interested in the deeper details of how I find vertices. There are likely more efficient solutions, but I think this works good enough for me :)

Click to expand the python code...

Imports:

from itertools import combinations_with_replacement, permutations
from fractions import Fraction as F

Constraints

# Range of polygon count at vertex
m_min = 3
m_max = 6
# Range of n-gon n at vertex
n_min = 3
n_max = [42, 12, 6, 3]

Fucntions

def n_gon(n: str) -> F:
    """Make n-gon interior angle as fraction of full turn"""
    return F(n-2, 2*n)


def rotrev(s) -> tuple[int]:
    """Generate all rotations and mirrors of s"""
    d = deque(s)
    for i in range(len(d)):
        d.rotate(1)
        yield tuple(d)
        yield tuple(reversed(d))

        
def find_vertices() -> list[tuple[int]]:
    """Find vertices"""
    found = []
    # Loop over number of n-gons
    for i, m in enumerate(range(m_min, m_max+1)):
        # Loop over all possible vertex candidates
        for comb in combinations_with_replacement(range(m_min, n_max[m-n_min]+1), r=m):            
            # Only consider proper vertices
            if sum(n_gon(c) for c in comb) != 1:
                continue
            # Add permutations 
            for p in permutations(comb):
                # Reject rotated or reversed forms
                if any(d in found for d in rotrev(p)):
                    continue
                found.append(p)
    return found

Running the search takes less than a seconds on my laptop

vertices = find_vertices()

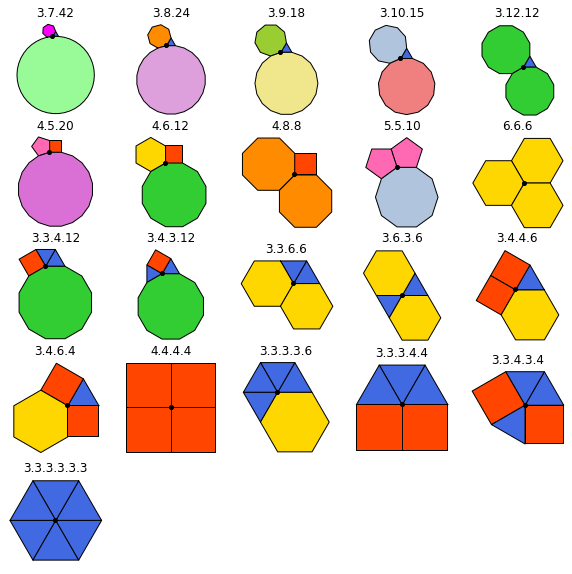
Search result

This table was made processing the resulting vertex list. Here \(m\) still is the number of polygons, each integer column the counts for a particular shape, and \(u\) the number of unique shapes.

vertex	\(m\)	3	4	5	6	7	8	9	10	12	15	18	20	24	42	\(u\)
3.7.42	3	1	0	0	0	1	0	0	0	0	0	0	0	0	1	3
3.8.24	3	1	0	0	0	0	1	0	0	0	0	0	0	1	0	3
3.9.18	3	1	0	0	0	0	0	1	0	0	0	1	0	0	0	3
3.10.15	3	1	0	0	0	0	0	0	1	0	1	0	0	0	0	3
3.12.12	3	1	0	0	0	0	0	0	0	2	0	0	0	0	0	2
4.5.20	3	0	1	1	0	0	0	0	0	0	0	0	1	0	0	3
4.6.12	3	0	1	0	1	0	0	0	0	1	0	0	0	0	0	3
4.8.8	3	0	1	0	0	0	2	0	0	0	0	0	0	0	0	2
5.5.10	3	0	0	2	0	0	0	0	1	0	0	0	0	0	0	2
6.6.6	3	0	0	0	3	0	0	0	0	0	0	0	0	0	0	1
3.3.4.12	4	2	1	0	0	0	0	0	0	1	0	0	0	0	0	3
3.4.3.12	4	2	1	0	0	0	0	0	0	1	0	0	0	0	0	3
3.3.6.6	4	2	0	0	2	0	0	0	0	0	0	0	0	0	0	2
3.6.3.6	4	2	0	0	2	0	0	0	0	0	0	0	0	0	0	2
3.4.4.6	4	1	2	0	1	0	0	0	0	0	0	0	0	0	0	3
3.4.6.4	4	1	2	0	1	0	0	0	0	0	0	0	0	0	0	3
4.4.4.4	4	0	4	0	0	0	0	0	0	0	0	0	0	0	0	1
3.3.3.3.6	5	4	0	0	1	0	0	0	0	0	0	0	0	0	0	2
3.3.3.4.4	5	3	2	0	0	0	0	0	0	0	0	0	0	0	0	2
3.3.4.3.4	5	3	2	0	0	0	0	0	0	0	0	0	0	0	0	2
3.3.3.3.3.3	6	6	0	0	0	0	0	0	0	0	0	0	0	0	0	1
total	-	15	10	2	7	1	2	1	2	4	1	1	1	1	1	-

Noteworthy observations

There are a total of 21 vertices (10 \(m=3\), 7 \(m=4\), 3 \(m=5\), 1 \(m=6\))
There are 1-3 polygon types in a vertex (10 \(u=3\), 8 \(u=2\), 3 \(u=1\))
The three single polygon type vertices are triangles, squares, and hexagons - the only three ways to tile the plane with a single polygon type!
Only 3-, 4-, 5-, 6-, 8-, 10- and 12-gons occur in more than one vertex
- 5 and 10 only ever occurr together
- 15 vertices contains triangles, 10 squares, 7 hexagons, and 4 dodecagons

Below is the code I used to generate the table and insights

Click to expand the python code...

Imports (in addition to above code)

import pandas as pd

Functions

def vertex_str(vtx: tuple[int]) -> str:
    """Make vertex notation from ints."""
    return '.'.join(map(str, vtx))    

def make_df(vertices: list[tuple[int]]) -> pd.DataFrame:
    """Make data frame with vertex summary."""
    vertices = find_vertices()
    ngons = {i for j in vertices for i in j}
    df = pd.DataFrame({"m": len(f), "vertex": f} for f in vertices)
    for ngon in {i for j in vertices for i in j}:
        df[ngon] = df["vertex"].apply(lambda x: list(x).count(ngon))
    df["vertex"] = df["vertex"].apply(vertex_str)
    df = df.set_index("vertex")[["m"]+sorted(list(ngons))]
    df["u"] = (df[list(ngons)]>0).sum(axis=1)
    df.loc["n_vertices"]=(df>0).sum()
    return df

Running

df=make_df(vertices)
print(df)
print(df[:-1]["m"].value_counts())
print(df[:-1]["u"].value_counts())

Drawing vertices

To draw vertices correctly, I define a polygon by \(n\) and one side. Swapping the side start and end points mirrors the polygon.

Click to expand the python code...

Imports

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from matplotlib.collections import PatchCollection

Functions

def make_patch(points: np.ndarray, ax, fc="white"):
    """Helper to draw polygon patch to ax"""
    ax.add_collection(
         PatchCollection([mpatches.Polygon(points)], fc=fc, ec='k',lw=1)
    )
    
def coords(n:int, line: np.ndarray) -> np.ndarray:
    """
    Args:
        * n (int) - n in n-gon
        * line (np.array) - ((x0,y0), (x1,y1)) line segment
    Returns:
        np.ndarray: shape (n, 2) x,y coordinate pairs
        
    """
    d = np.diff(line.T, axis=1)
    r = np.linalg.norm(d)
    a = np.arange(n)*(
        np.pi-np.pi*2*float(n_gon(n)))+\
        np.arctan2(d[0], d[1])
    p = line[0][:, None]
    return np.hstack(((p+np.cumsum(
        r*np.array([np.sin(a), np.cos(a)]),
        axis=1)), p)).T

Colors

colors = {
"royalblue", 
"orangered", 
"hotpink", 
"gold", 
"magenta", 
"darkorange", 
"yellowgreen", 
"lightsteelblue", 
"limegreen",
"lightcoral",
"khaki",
"orchid",
"plum",
"palegreen",
}

Running

fig, axs = plt.subplots(5,5,figsize=(10,10))
axs = axs.flatten()  # all subplits as list

g0 = np.array([[1,0],[0,0]])  # line to start with
for i, vertex in enumerate(vertices):
    ax = axs[i]
    ps = [] # save coordinates for bounding box
    ax.plot(0, 0,"ko", ms=4) # Draw vertex
    # Add polygons
    for gon in vertex:
        p = coords(gon, g0)
        ps.extend(p.tolist())
        make_patch(p, ax, colors[gon])
        g0 = p[:2][::-1] # move starting line for next iteration
    # Bounding box
    xmin, ymin = np.min(ps, axis=0)*1.05
    xmax, ymax = np.max(ps, axis=0)*1.05
    ax.set(title=vertex_str(vertex), xlim=(xmin,xmax), ylim=(ymin,ymax));

# Ensure equal aspect and no axes for all plots
for i in range(i, 5*5):
    ax = axs[i]
    ax.set_aspect('equal', adjustable='box')
    ax.axis('off')

# Save result
fig.savefig("vertices.png", facecolor='white', transparent=False, bbox_inches="tight")