Fun with fish tiles

This article was featured in Mitteiling der Meutschen Mathematiker-Vereingung¹.

The fish tile

A fish tile is shown in Figure 1. It is remarkably fun to play with! It is formed by two equilateral pentagons - the regular pentagon head, and the pentagonal crescent tail. The tail opening angle is 108 degrees so it fits a regular pentagon, while the angle between the head and tail is 144 degrees and fits a regular decagon.

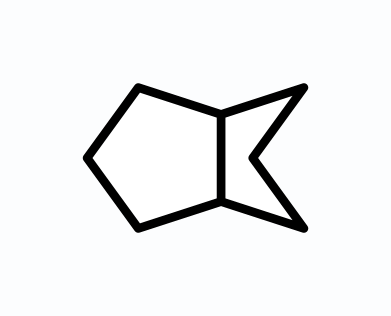
All of the images in this post were made using the excellent Girih App. For the Escher like cartoon on top, I added fish faces in Affinity designer, and for the big tiling at the end I used Affinity photo to add a background gradient, a signature and some drop shadow.

Fish rings

Two regular pentarings of five fish are shown in Figure 2. In the first one, heads connect to the side of the tail forming a central star, and in the second one, heads go inside the tail to form a pentagon. I think these are the only possible pentarings of fish.

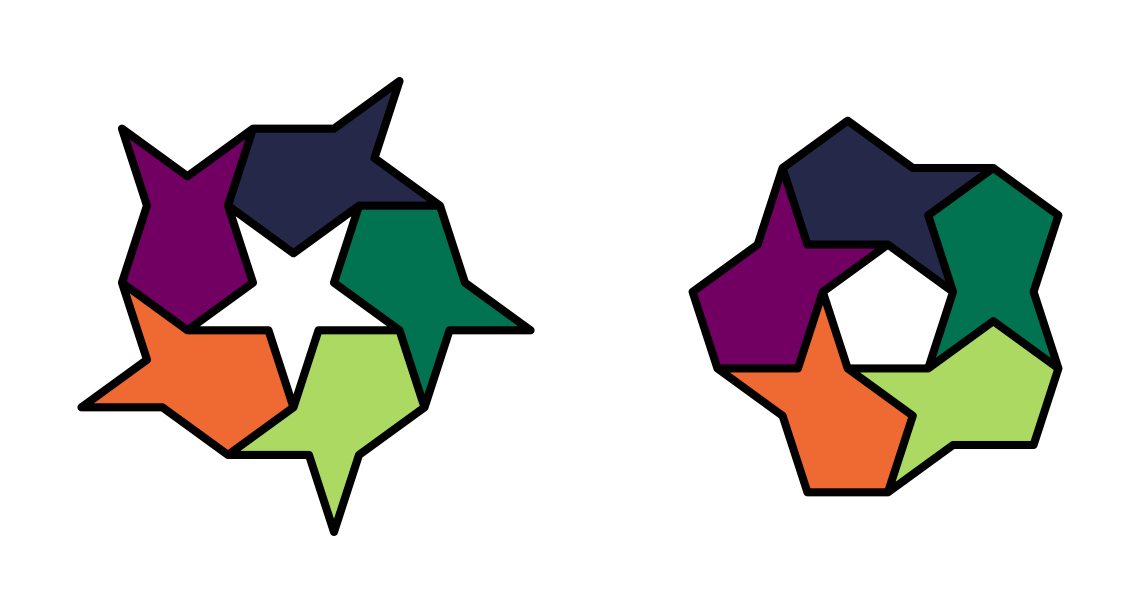
Similarly, there are decarings, shown in Figure 3.. First a decagon formed by tiling heads in 5.5.10 vertices, next a star is formed by putting heads together, and finally a large pentagon is formed by flipping the heads in the star tiling.

Tiling the plane

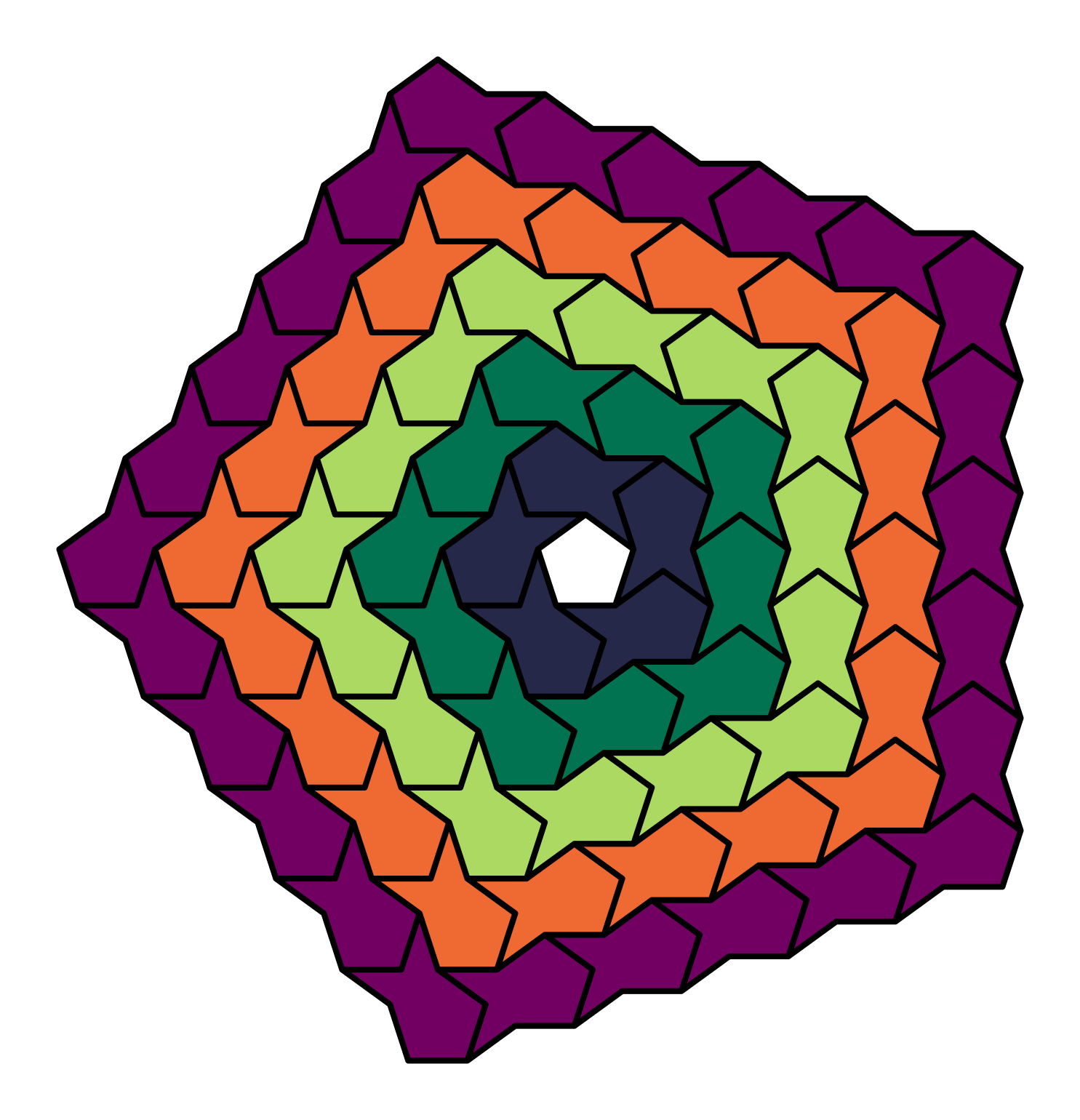
By making concentric pentarings, all of the plane except the central pengagon can be tiled, as shown in Figure 4.. However, by tiling fishes head to tail on straight lines tilings over the full plane can be achived. Lines fit together regardless of swimming direction, as shown in the two examples pineapple fish examples shown in Figure 5. The second tiling, is identical to the one used in the cartoon header of this blog post.

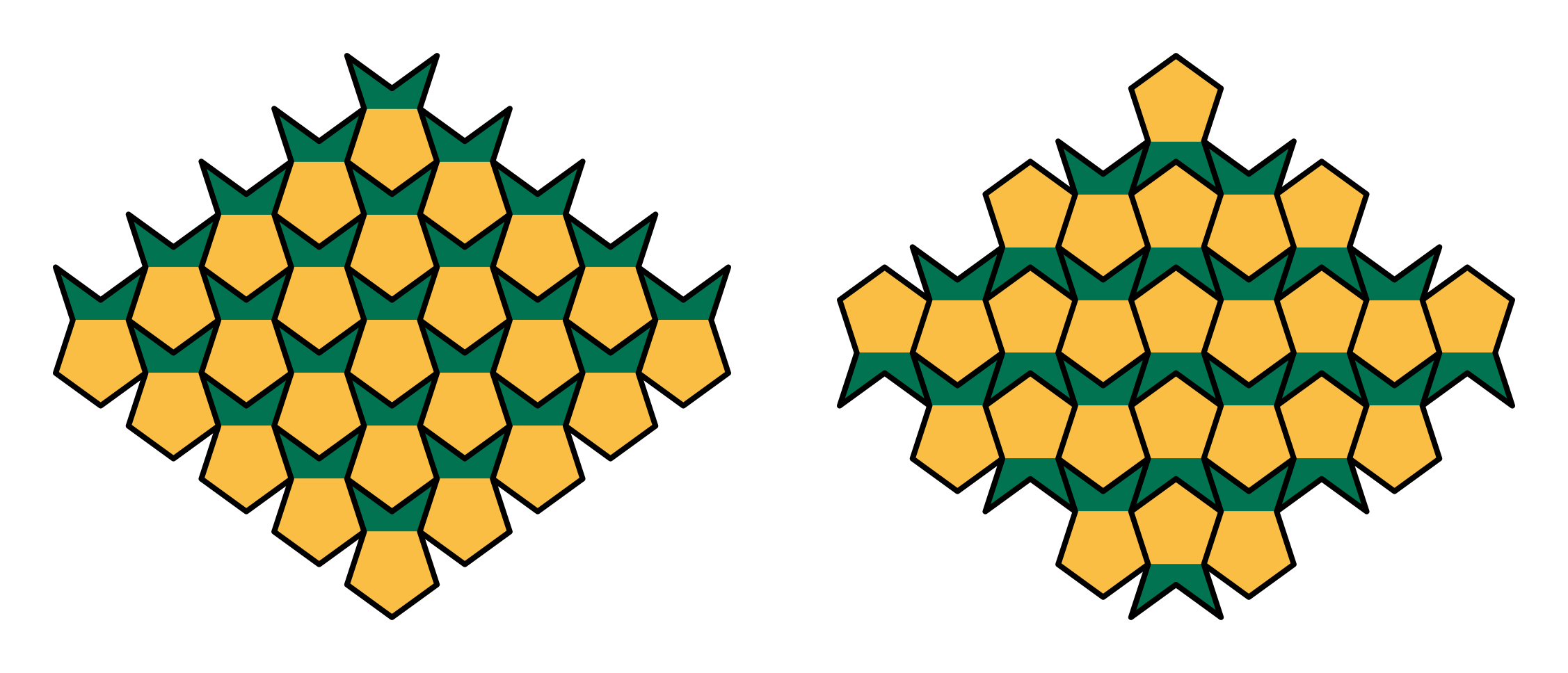
Big tiling

Finally, in Figure 6., is a tiling (with holes) using the pentaring from Figure 1.. In addition to the pentagonal holes, this tiling has squiggly rhombic holes, with pointy angles 1/10 of a full turn.